[Data Structures] 정렬 (Sorting)

1. 버블 정렬 (Bubble Sort) 

• 인접한 두 개의 데이터를 비교해가면서 정렬을 진행
• 앞에서부터 순서대로 비교하고 교환하는 일련의 과정이 거품이 일어나는 모습에 비유되어 버블정렬이라 함
• 이해를 위한 그림 및 성능평가

출처: https://slidesplayer.org/slide/14647376/

 

 

 

2. 선택 정렬 (Selection Sort) 

• 정렬순서에 맞게 하나씩 선택해서 옮기는, 옮기면서 정렬이 되게 하는 알고리즘
• 정렬순서상 가장 앞서는 것을 선택해서 가장 왼쪽으로 이동시키고, 원래 그 자리에 있던 데이터는 빈 자리에 가져다 놓는다
• 이해를 위한 그림 및 성능평가

출처: https://slidesplayer.org/slide/14647376/

 

 

 

3. 삽입 정렬 (Insertion Sort) 

• 정렬 대상을 두 부분으로 나눠서, 정렬 안 된 부분에 있는 데이터를 정렬 된 부분의 특정 위치에 삽입해 가면서 정렬을 진행하는 알고리즘
• 데이터를 한 칸씩 뒤로 밀면서 삽입할 위치를 찾는다

출처: https://slidesplayer.org/slide/14647376/

 

 

 

 

4. 힙 정렬 (Heap Sort)

•  힙 정렬의 특성 : 힙의 루트 노드에 저장된 값이 가장 커야 한다
• 이를 활용하면 "힙의 루트 노드에 저장된 값이 정렬 순서상 가장 앞선다" 로 구성할 수 있다 

출처: https://slidesplayer.org/slide/14647376/

 

 

 

 

5. 병합 정렬 (Merge Sort)

• 분할 정복 (Divide and Conquer) 이라는 알고리즘 디자인 기법에 근거해 만들어진 정렬 방법
• 총 3단계
  1. 분할 (Divide) - 해결이 용이한 단계까지 문제를 분할해 나간다
  2. 정복 (Conquer) - 해결이 용이한 수준까지 분할된 문제를 해결한다
  3. 결합 (Combine) - 분할해서 해결한 결과를 결합하여 마무리한다 
   

출처: https://slidesplayer.org/slide/14647376/

 

 

 

 

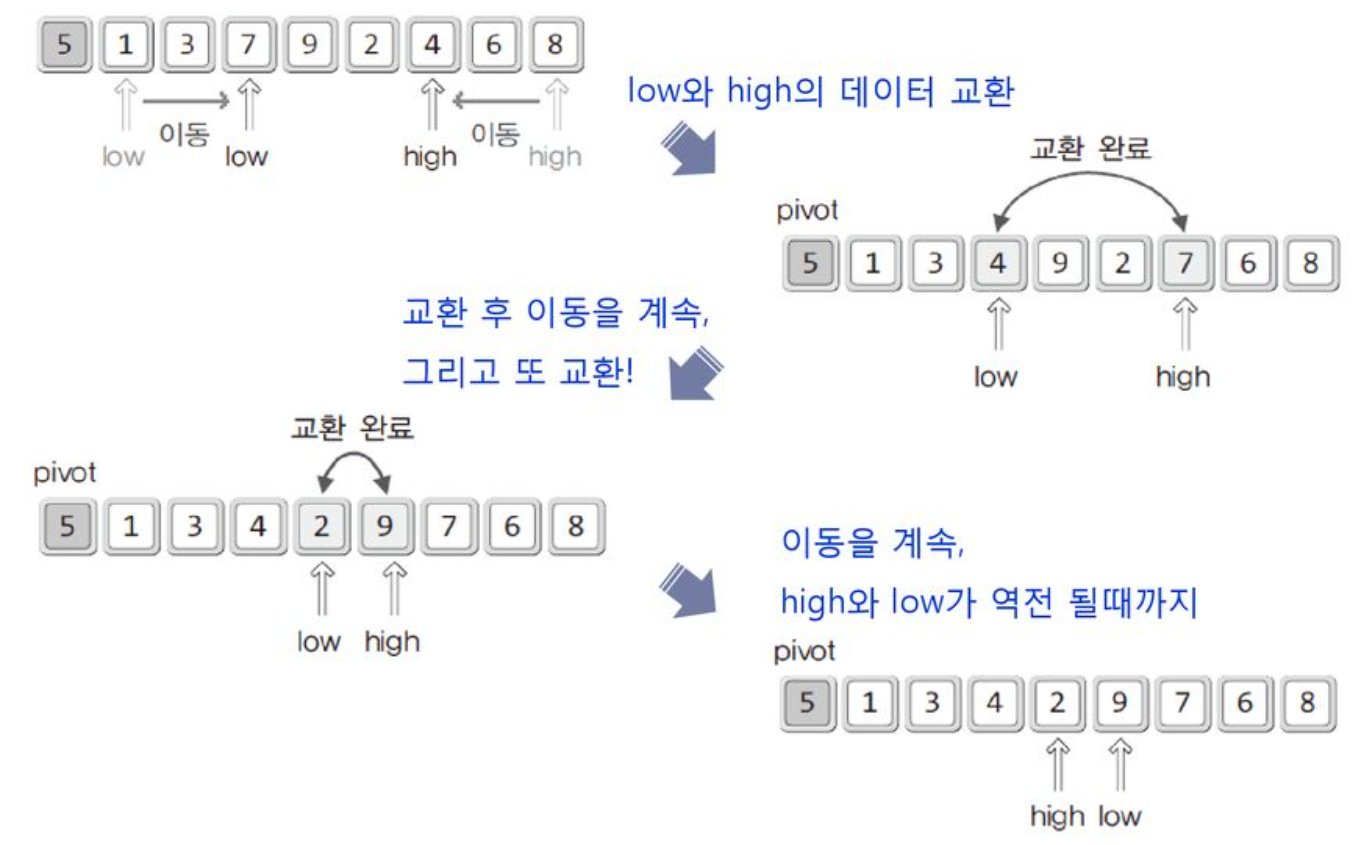
6. 퀵 정렬 (Quick Sort)

• 퀵 정렬 이해에 필요한 정의
  1. left - 정렬대상의 가장 왼쪽 지점
  2. right - 정렬대상의 가장 오른쪽 지점
  3. pivot - 중심점, 중심축의 의미를 담고있음
  4. low - 피벗을 제외한 가장 왼쪽에 위치한 지점
  5. high - 피벗을 제외한 가장 오른쪽에 위치한 지점
   

출처: https://slidesplayer.org/slide/14647376/

 

 

 

 

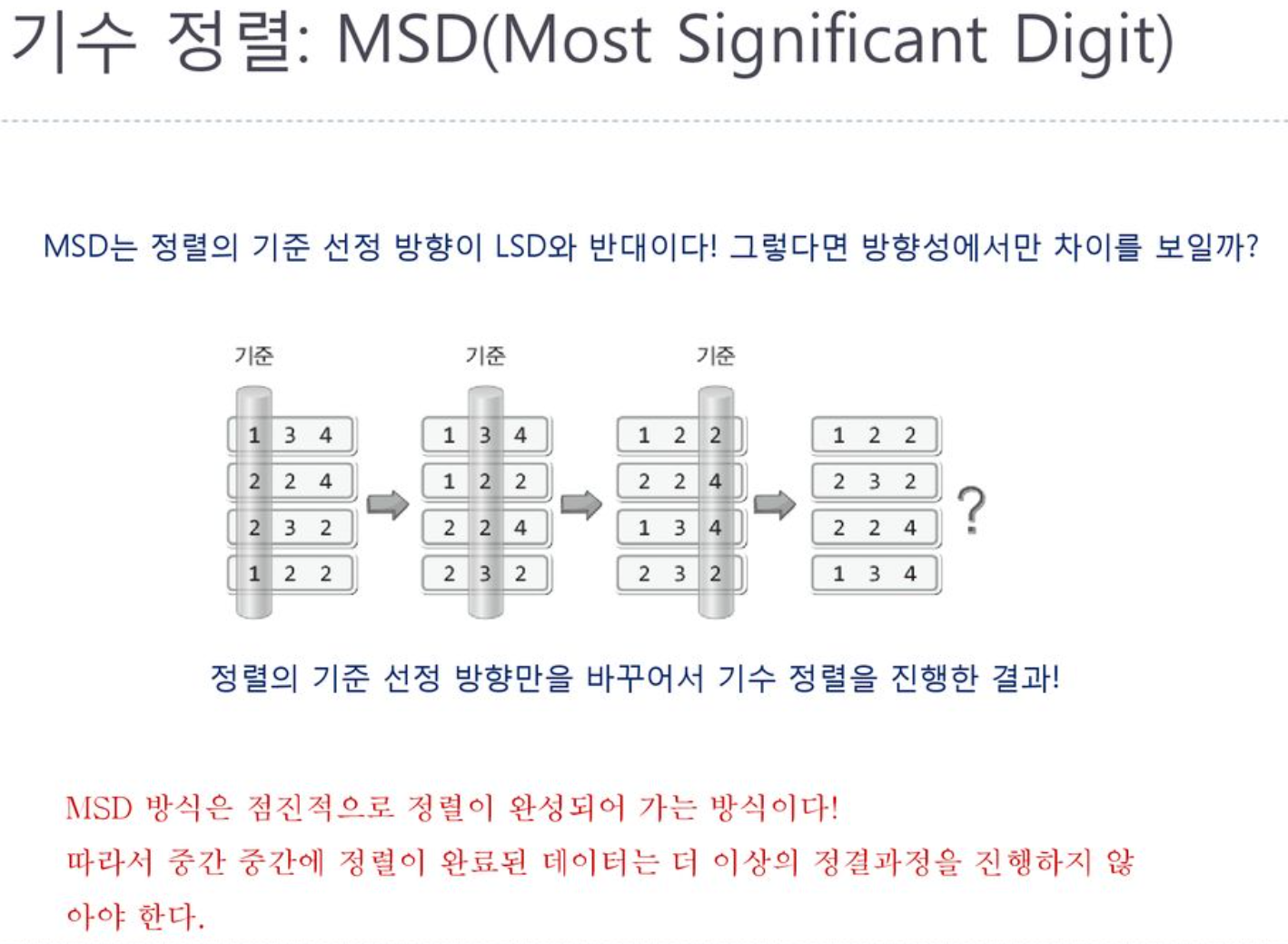
7. 기수 정렬 (Radix Sort)

출처: https://slidesplayer.org/slide/14647376/

#include <stdio.h>
#include "ListBaseQueue.h"
 
#define BUCKET_NUM 10
 
void RadixSort(int arr[],int num, int maxLen)
{
    // 매개변수 maxLen에는 정렬대상 중 가장 긴 데이터의 길이 정보가 전달
    Queue bukets[BUCKET_NUM];
    int bi;
    int pos;
    int di;
    int divfac = 1;
    int radix;
    
    // 10 개의 버킷 초기화
    for(bi =0; bi<BUCKET_NUM; bi++)
        QueueInit(&bukets[bi]);
    
    //가장 긴 데이터의 길이만큼 반복
    for(pos=0;pos<maxLen;pos++)
    {
        //정렬대상의 수만큼 반복
        for(di=0;di<num;di++)
        {
            //N번째 자리의 숫자 추출
            radix = (arr[di]/divfac)%10;
            
            // 추출한 숫자를 근거로 법킷에 데이터 저장
            Enqueue(&bukets[radix], arr[di]);
        }
        
        //  버킷 수만큼 반복
        for(bi=0,di=0;bi<BUCKET_NUM;bi++)
        {
            //버킷에 저장된 것 순서대로 다 꺼내서 다시 arr에 저장
            while(!QIsEmpty(&bukets[bi]))
                arr[di++] = Dequeue(&bukets[bi]);
        }
        
        // N번째 자리의 숫자 추출을 위한 피제수 증가
        divfac *= 10;
    }
}
 
int main(void)
{
    int arr[7]={13,212,14,7141,10987,6,15};
    
    int len = sizeof(arr)/sizeof(int);
    int i;
    ;
    RadixSort(arr, len, 5);
    
    for(i=0;i<len;i++)
        printf("%d ",arr[i]);
    printf("\n");
    return 0;
}