1. 테이블 (Table) 자료구조의 이해
- 탐색대상을 단번에 찾을 수 있는 자료구조로, O(1)의 시간복잡도를 가진다
- 저장되는 데이터는 키(key)와 값(value)이 하나의 쌍을 이룬다
- 키(key)가 존재하지 않는 값은 저장할 수 없다
- 모든 키(key)는 중복되지 않는다
- map 으로 불리기도 한다
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
//"UnderstandTable.c"
typedef struct _empInfo
{
int empNum; //직원의 고유번호
int age; //직원의 나이
} EmpInfo;
int main(void)
{
EmpInfo empInfoArr[1000];
EmpInfo ei;
int eNum;
printf("사번과 나이 입력: ");
scanf("%d %d", &(ei.empNum), &(ei.age));
empInfoArr[ei.empNum] = ei; //단번에 저장
printf("확인하고픈 직원의 사번 입력: ");
scanf("%d", &eNum);
ei = empInfoArr[eNum]; //단번에 탐색
return 0;
}
|
cs |
2. 해쉬(Hash) 의 필요성
- 문제점: 직원 고유번호의 범위가 1000000~9999999라면 위와 같은 방식으로 데이터를 구성하려면 매우 큰 배열이 필요하다
- 예를 들어, 입사 직원의 고유번호가 입사년도+입사순서 로 구성된다면 ex) 20120003, 20120004... 이러한 직원의 고유번호를 활용해서 가공의 과정을 거친다

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
//"TableHashFunction.c"
typedef strcut _empInfo
{
int empNum; // 직원의 고유번호
int age; // 직원의 나이
} EmpInfo;
//해쉬 함수 - 넓은 범위의 키를 좁은 범위의 키로 변경하는 역할 //여덞 자리의 수로 이뤄진 직원의 고유번호를 두 자리의 수로 변경한다
int GetHashValue(int empNum)
{
return empNum % 100;
}
int main(void)
{
EmpInfo empInfoArr[100];
EmpInfo emp1={20120003, 42};
EmpInfo emp2={20130012, 33};
EmpInfo r1, r2;
//키를 인덱스 값으로 이용해서 저장
empInfoArr[GetHashValue(emp1.empNum)] = emp1;
//키를 인덱스 값으로 이용해서 탐색
r1 = empInfoArr[GetHashValue(20120003)];
return 0;
}
|
cs |
3. 해쉬(Hash)의 충돌 상황 해결법
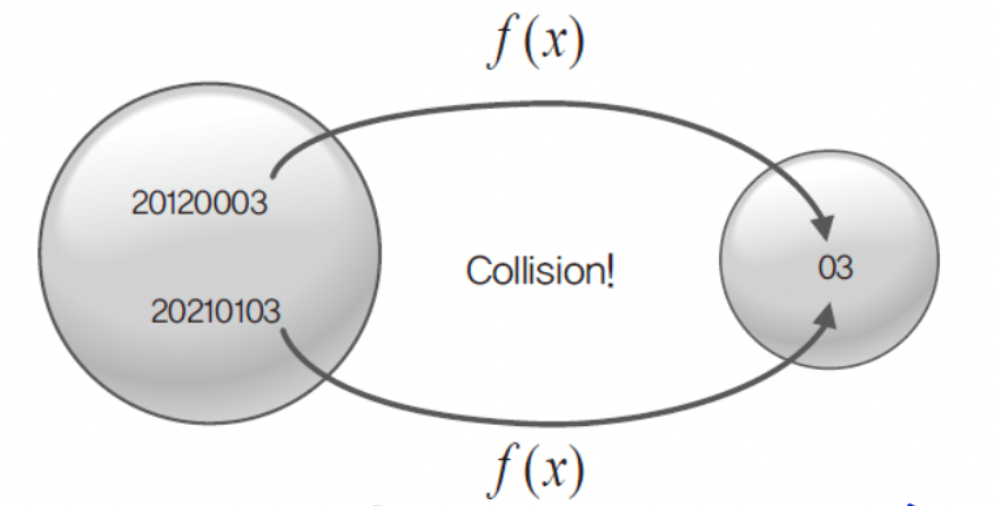
- 예를 들어, 위의 예에서 직원의 수가 100명이 넘어가면서 해쉬 함수를 적용 했을 때 동일한 결과를 가져오는 경우가 생기는 상황을 '충돌' 이라고 한다
- 좋은 해쉬 함수란? 데이터가 테이블의 전체 영역에 골고루 분포될 수 있는 함수, 충돌을 덜 일으키는 함수, 키 전체를 참조하여 해쉬 값을 만들어 낸다.
- 좋지 못한 해쉬 함수는 테이블의 특정 영역에 데이터가 몰리는 상황을 보여준다. 그만큼 충돌이 발생할 확률이 높다.

- 좋은 해쉬 함수 디자인 방법들
- 자릿수 선택 (Digit Selection) : 예를 들어, 여덞 자리의 수로 이뤄진 키에서 다양한 해쉬 값 생성에 도움을 주는 네 자리의 수를 뽑아서 해쉬 값을 생성한다. 키의 특정 위치에서 중복의 비율이 높거나 아예 공통으로 들어가는 값이 있다면, 이를 제외한 나머지를 가지고 해쉬 값을 생성한다
- 비트 추출 방법 : 탐색 키의 비트 열에서 일부를 추출 및 조합하는 방법
- 자릿수 폴딩 (Digit Folding) : 예를 들어, 다음 그림의 숫자를 삼등분 하여 접어서 숫자를 겹치가 만든다. 이렇게 겹친 두 자릿수 숫자를 모두 더하여 그 결과를 해쉬 값으로 결정하는 방법이다.
- 이외에도, 키를 제곱하여 그 중 일부를 추출하는 법, 폴딩의 과정에서 덧셈 대신 XOR 연산을 하는 법, 통계적으로 넓은 분포를 보이는 다양한 방법 등이 있다
- 충돌 문제의 해결책
- 1. 선형 조사법 (Linear Probing) - 충돌이 발생했을 때, 옆자리가 비었는지 보고 비었을 경우 그 자리에 대신 저장하는 방법. 옆자리가 비어있지 않은 경우, 한 칸 더 이동을 해서 자리를 살피게 된다.
- 하지만 충돌의 횟수가 증가함에 따라서 클러스터 현상, 특정 영역에 데이터가 집중적으로 몰리는 현상이 발생한다 -> 이는 충돌의 확률을 높이는 직접적인 원인이 된다

2. 이차 조사법 (Quadratic Probing) - 선형 조사법의 문제를 해결하기 위해 등장한 방법. 바로 옆이 아니라 조금 멀리서 빈 공간을 찾아 살피는 방법

3. 슬롯의 상태 정보 별도 관리의 필요성
- EMPTY (이 슬롯에는 데이터가 저장된 바 없다)
- DELETED (이 슬롯에는 데이터가 저장된바 있으나 현재는 비워진 상태다)
- INUSE (이 슬롯에는 현재 유효한 데이터가 저장되어 있다)
- DELETED 와 EMPTY로 구분하는 이유는, 탐색할 때 그 위치의 슬롯 상태가 EMPTY라면 데이터가 존재하지 않는다고 판단해 옆자리도 확인해보지 않고 종료하게 된다. 따라서 DELETED 상태임을 확인한다면 충돌이 발생했음을 의심하여 선형 조사법에 근거한 탐색의 과정을 진행한다.
4. 정리
- 선형, 이차 조사법과 같은 충돌의 해결책 적용을 위해서는, 슬롯의 상태에 DELETED를 포함시켜야 한다
- 선형, 이차 조사법을 적용했다면, 탐색의 과정에서도 이를 근거로 충돌을 의심하는 탐색의 과정을 포함시켜야 한다
5. 이중 해쉬 (Double Hash)
- 이차 조사법의 문제점: 해쉬 값이 같으면 충돌 발생시 빈 슬롯을 찾기 위해서 접근하는 위치가 늘 동일하다
- 이를 해결하기 위해 불규칙하게 구성하게 됨
- 1차 해쉬 함수 - 키를 근거로 저장위치를 결정하기 위한 것
- 2차 해쉬 함수 - 충돌 발생시 몇 칸 뒤를 살필지 결정하기 위한 것


6. 체이닝 (Chaining)
- 위의 방법들은 열린 어드레싱 방법으로 충돌이 발생하면 다른 자리에 대신 저장한다는 의미
- 체이닝은 닫힌 어드레싱 방법으로 무슨 일이 있어도 자신의 자리에 저장을 한다는 의미 -> 자리를 여러 개 마련한다
- 배열을 이용하는 법 - 해쉬 값 별로 다수의 슬롯을 마련할 수 있으나 충돌이 발생하지 않을 경우 메모리 낭비가 심하다는 단점이 있다

2. 연결 리스트를 이용하는 법 - 슬롯을 생성하여 연결 리스트의 모델로 연결해나가는 방식, 하나의 해쉬 값에 다수의 슬롯을 둘 수 있다. 따라서 탐색을 위해서는 동일한 해쉬 값으로 묶여있는 연결된 슬롯을 모두 조사해야 한다는 불편이 따른다.

728x90
'Data Structures & Algorithms' 카테고리의 다른 글
| [Algorithms] Basic-대표값 찾기 (0) | 2022.05.12 |
|---|---|
| [Data Structures] 그래프 (Graph) (0) | 2022.05.10 |
| [Data Structures] 탐색 (Search) (0) | 2022.05.09 |
| [Data Structures] 정렬 (Sorting) (0) | 2022.05.09 |
| [Data Structures] 우선순위 큐 (Priority Queue)와 힙 (Heap) (0) | 2022.05.07 |