1. 보간 탐색 (Interpolation Search)
- 기존 두 가지 탐색 알고리즘
- 순차 탐색 - 정렬되지 않은 대상을 기반으로 하는 탐색
- 이진 탐색 - 정렬된 대상을 기반으로 하는 탐색
- 이 중에서 이진 탐색은 중앙에 위치한 데이터를 탐색한 후, 이를 기준으로 탐색대상을 반씩 줄여나가면서 탐색을 진행하는 알고리즘. 찾는 대상이 중앙에 위치하건 맨 앞에 위치하건 그에 상관하지 않고 일관되게 반씩 줄여나간다.
- 보간 탐색은 이를 개선시킨 알고리즘으로서 탐색대상이 앞쪽에 위치해 있으면 앞쪽에서 탐색을 시작하는 알고리즘
- 보간 탐색의 위치를 정하는 방법 - 데이터 값과 그 데이터가 저장된 위치의 인덱스 값이 비례한다고 가정

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
#include <stdio.h>
int ISearch(int ar[],int first,int last, int target)
{
int mid;
// target이 주어진 범위값에 존재하지 않는 경우 탈출하지 못하는 상황이 생긴다 // ex) int arr[] = {1,3,5,7,9}; ISearch(arr, 1, 4, 2) // 배열 arr의 인덱스 1~4 범위 내에서 숫자 2 탐색하면 탈출하지 못한다 // if(first > last)
// return -1;
// 따라서 새로운 탈출 조건 if(ar[first] > target || ar[last] < target) return -1; //이진 탐색과의 차이점을 반영한 문장
mid = ((double)(target-ar[first])/(ar[last]-ar[first])*(last-first))+first;
if(ar[mid]==target)
return mid;
else if(target<ar[mid])
return ISearch(ar, first, mid-1, target);
else
return ISearch(ar, mid+1, last, target);
}
|
cs |
2. 이진 탐색 트리 (Binary Search Tree)
- 이진 탐색 트리에는 데이터를 저장하는 규칙이 있다. 그 규칙은 특정 데이터의 위치를 찾는데 사용할 수 있다
- '이진 트리' + '데이터의 저장 규칙' = '이진 탐색 트리'
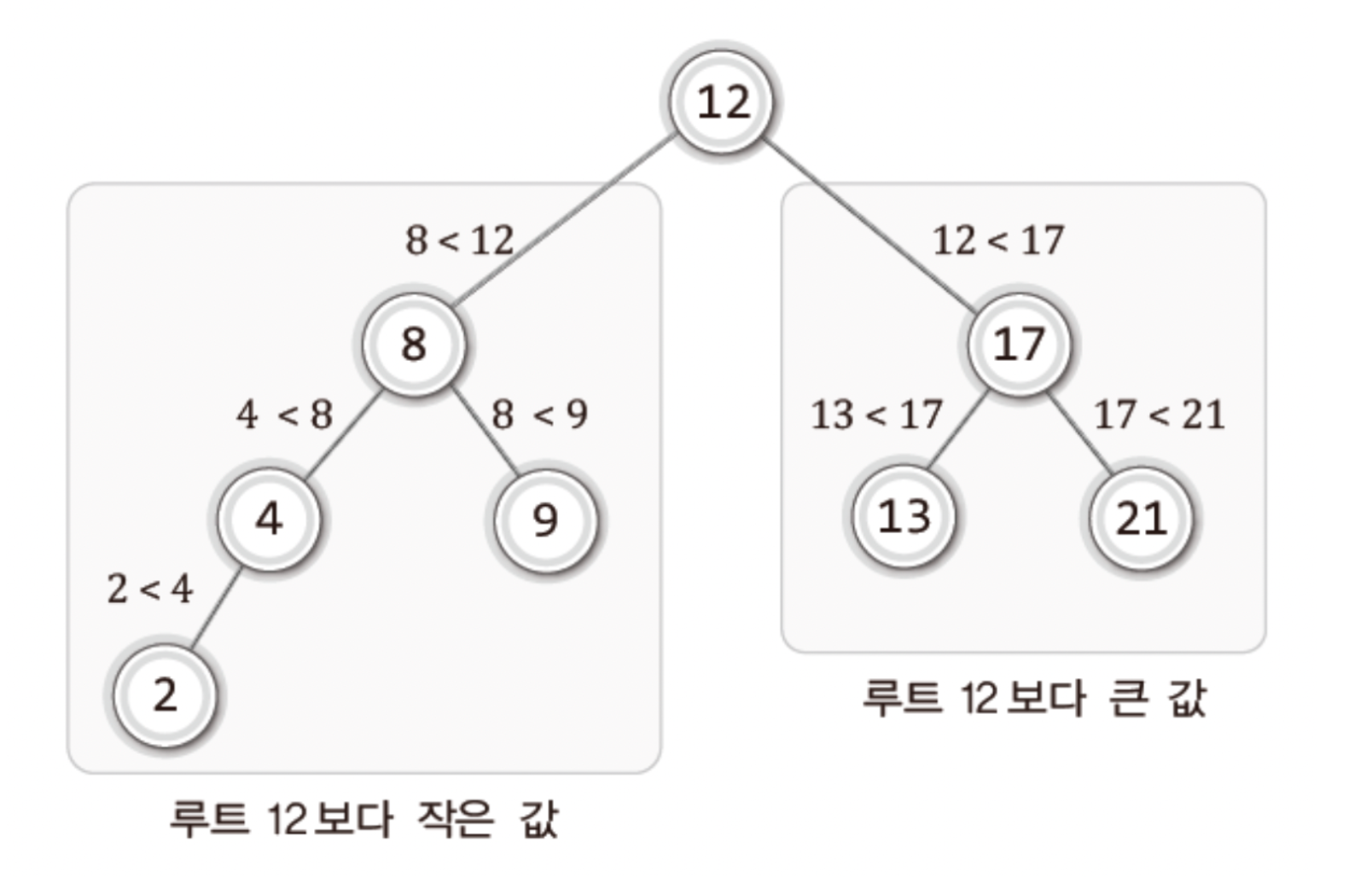
- 이진 탐색 트리의 노드에 저장된 키는 유일하다
- 루트 노드의 키가 왼쪽 서브 트리를 구성하는 어떠한 노드의 키보다 크다
- 루트 노드의 키가 오른쪽 서브 트리를 구성하는 어떠한 노드의 키보다 작다
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다
- 왼쪽 자식 노드의 키 < 부모 노드의 키 < 오른쪽 자식 노드의 키
- 이진 탐색 트리의 구현 방안 - 일전의 이진 트리 구현한 코드 + 새롭게 구현

- 이진 탐색 트리에 새로운 데이터 삽입 방법

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
|
#include <stdio.h>
#include "BinaryTree2.h"
#include "BinarySearchTree.h"
void BSTMakeAndInit(BTreeNode ** pRoot)
{
*pRoot = NULL;
}
BSTData BSTGetNodeData(BTreeNode * bst)
{
return GetData(bst);
}
void BSTInsert(BTreeNode ** pRoot, BSTData data)
{
BTreeNode * pNode = NULL; //parent Node
BTreeNode * cNode = *pRoot; // Current Node
BTreeNode * nNode = NULL; // New Node
// 새노드 저장될 위치 찾는다.
while(cNode != NULL)
{
if(data == GetData(cNode))
return; // 데이터 중복 허용 x
pNode = cNode; // 매번 while 문을 돌때마다 초기화가 된다.
if(GetData(cNode)>data)
{
cNode = GetLeftSubTree(cNode);
}
else
cNode = GetRightSubTree(cNode);
}
//pNode의 자식 노드로 추가할 새 노드의 생성
nNode = MakeBTreeNode(); // 새 노드 생성
SetData(nNode, data);
// pNode 의 자식 노드로 추가할 새 노드의 생성
if(pNode != NULL) // 새 노드가 루트노드아니라면
{
if(data < GetData(pNode))
MakeLeftSubTree(pNode, nNode);
else
MakeRightSubTree(pNode, nNode);
}
else{ //새노드가 루트노라면
*pRoot = nNode;
}
}
BTreeNode *BSTSearch(BTreeNode * bst, BSTData target)
{
BTreeNode * cNode = bst; // current Node
BSTData cd; // current Data
while(cNode != NULL)
{
cd = GetData(cNode);
if(target == cd)
return cNode;
else if(target<cd)
cNode = GetLeftSubTree(cNode);
else
cNode = GetRightSubTree(cNode);
}
return NULL;
}
|
cs |
- 이진 탐색 트리에 데이터 삭제 방법
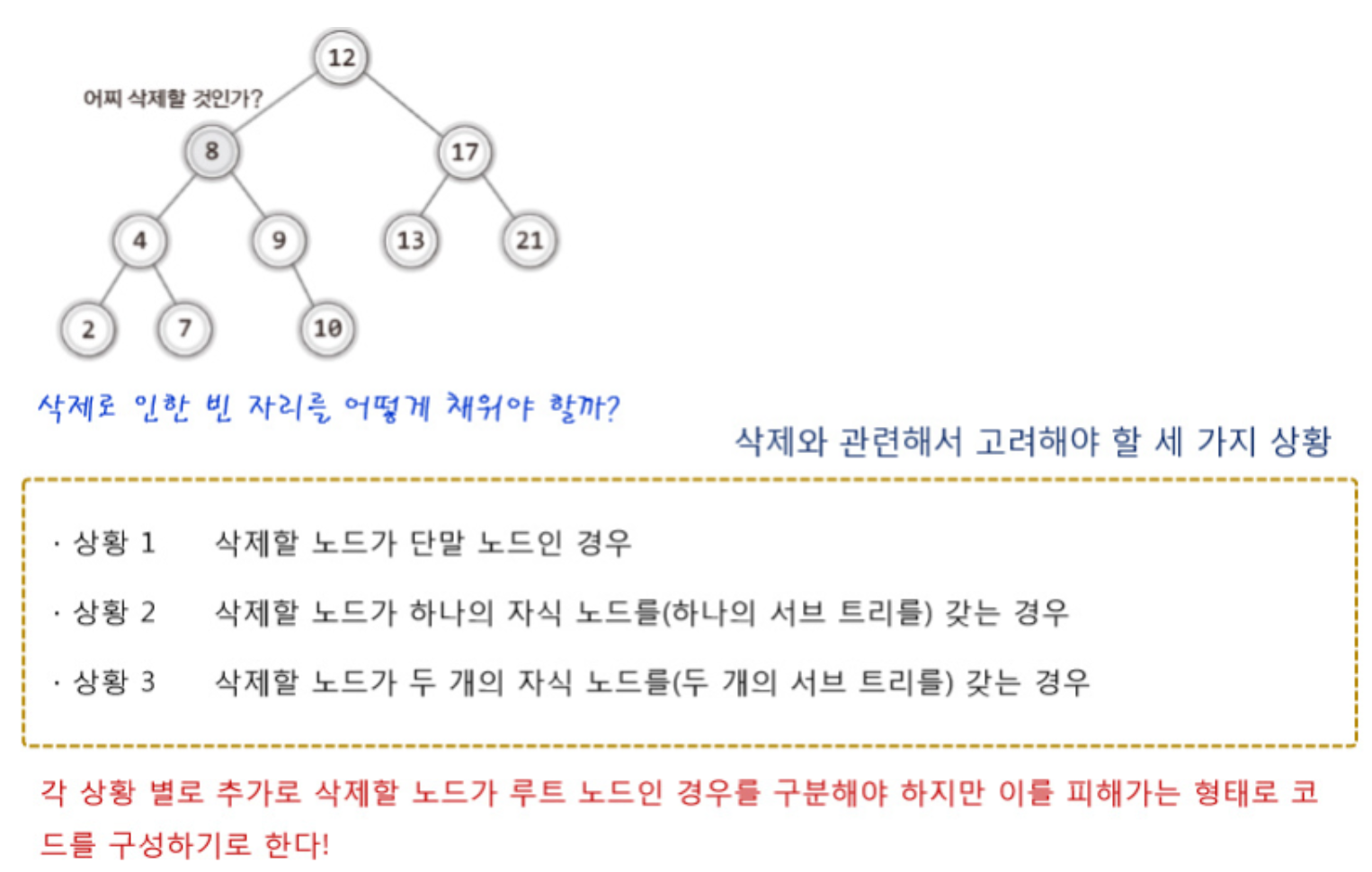
- 상황1


- 상황2


- 상황3 - 삭제할 노드의 오른쪽 서브 트리에서 가장 작은 값을 지니는 노드를 찾아서 이것으로 삭제할 노드를 대체한다
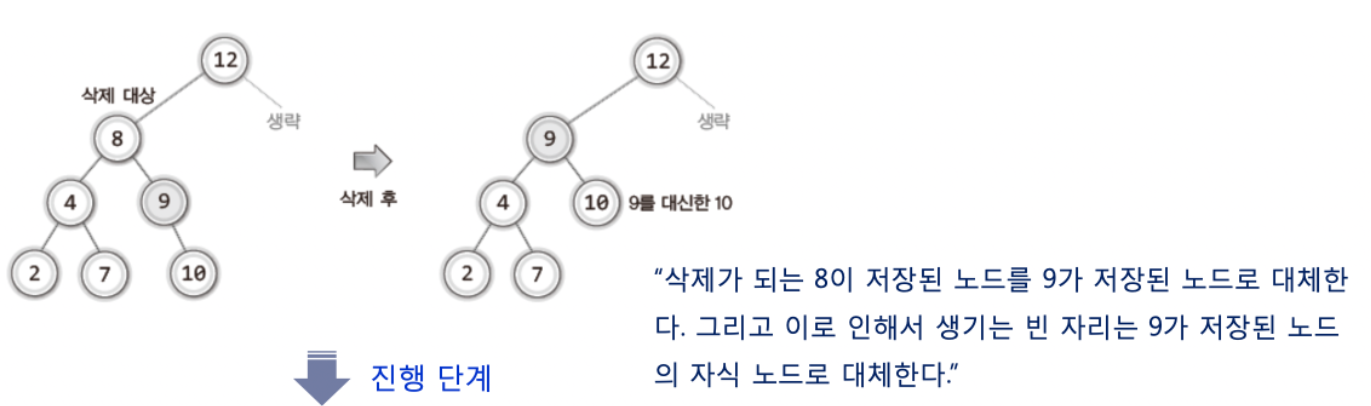

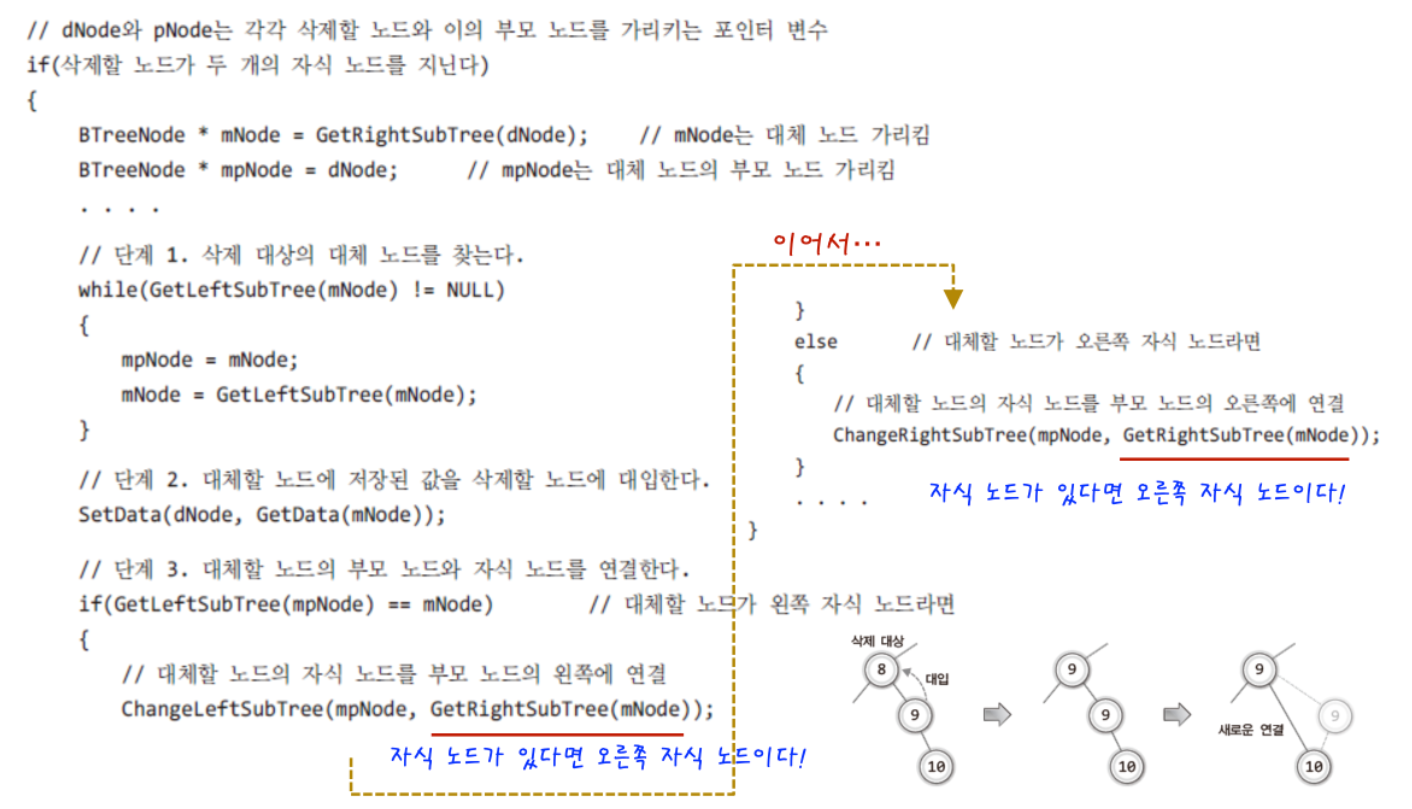
728x90
'Data Structures & Algorithms' 카테고리의 다른 글
| [Data Structures] 그래프 (Graph) (0) | 2022.05.10 |
|---|---|
| [Data Structures] 테이블(Table)과 해쉬(Hash) (0) | 2022.05.09 |
| [Data Structures] 정렬 (Sorting) (0) | 2022.05.09 |
| [Data Structures] 우선순위 큐 (Priority Queue)와 힙 (Heap) (0) | 2022.05.07 |
| [Data Structures] 트리 (Tree) (0) | 2022.05.07 |