1. 자료구조 vs 알고리즘
자료구조: 데이터의 표현 및 저장방법
알고리즘: 표현 및 저장된 데이터를 대상으로 하는 '문제의 해결 방법'
2. 자료구조의 분류

3. 시간 복잡도 (Time Complexity) & 공간 복잡도 (Space Complexity)
시간 복잡도: 알고리즘의 속도를 평가하는 요소
연산의 횟수를 통해서 빠르기 판단 / 데이터의 수 n에 대한 연산횟수의 함수 T(n)을 구성
공간 복잡도: 알고리즘의 메모리 사용량을 평가하는 요소
4. 순차 탐색 알고리즘 (Linear Search Algorithm)의 시간 복잡도 계산
- if(ar[i] == target) 핵심이 되는 연산을 중심으로 시간 복잡도를 계산
- Worst Case를 중심으로 알고리즘의 성능을 판단
- 데이터가 n개라고 가정하면 == 비교연산을 총 n번 진행하므로 T(n) = n
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <stdio.h>
int LSearch(int ar[], int len, int target)
{
int i;
for(i=0; i<len; i++)
{
if(ar[i] == target)
return i;
}
return -1;
}
int main(void)
{
int arr[] = {3,5,2,4,9};
int idx;
idx = LSearch(arr, sizeof(arr)/sizeof(int), 4)
if(idx == -1)
printf("Failed to search\n");
else
printf("Target Index: %d\n", idx);
return 0;
}
|
|
|
5. 이진 탐색 알고리즘 (Binary Search Algorithm)의 시간 복잡도 계산 - ***이진 탐색 알고리즘을 이용하려면 저장된 데이터가 정렬되어 있어야 한다***

- if(ar[mid]==target) 비교연산이 연산횟수를 대표하는 연산
- 데이터의 수 n이 1이 되기까지 2로 나눈 횟수 k회 + 데이터가 1개 남았을 때의 비교연산 1회 진행 T(n)=k+1
- n이 1이 되기까지 (1/2)로 나눈 횟수가 k이므로 T(n) = log₂n
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include <stdio.h>
int BSearch(int ar[], int len, int target)
{
int first = 0;
int last = len-1;
int mid;
while(first<=last)
{
mid = (first+last)/2;
if(ar[mid]==target){
return mid;
}
else{
if(ar[mid] > target)
last = mid-1;
else
first = mid+1;
}
}
return -1;
}
int main(void)
{
int arr[] = {1,3,5,7,9};
int idx;
idx = BSearch(arr, sizeof(arr)/sizeof(int), 7)
if(idx == -1)
printf("Failed to search\n");
else
printf("Target Index: %d\n", idx);
idx = BSearch(arr, sizeof(arr)/sizeof(int), 4)
if(idx == -1)
printf("Failed to search\n");
else
printf("Target Index: %d\n", idx);
return 0;
}
|
cs |
6. 빅-오 표기법 (Big-Oh Notation)
함수 T(n)에서 가장 영향력이 큰 부분이 어딘가를 따져 시간복잡도 함수를 구하는 방법
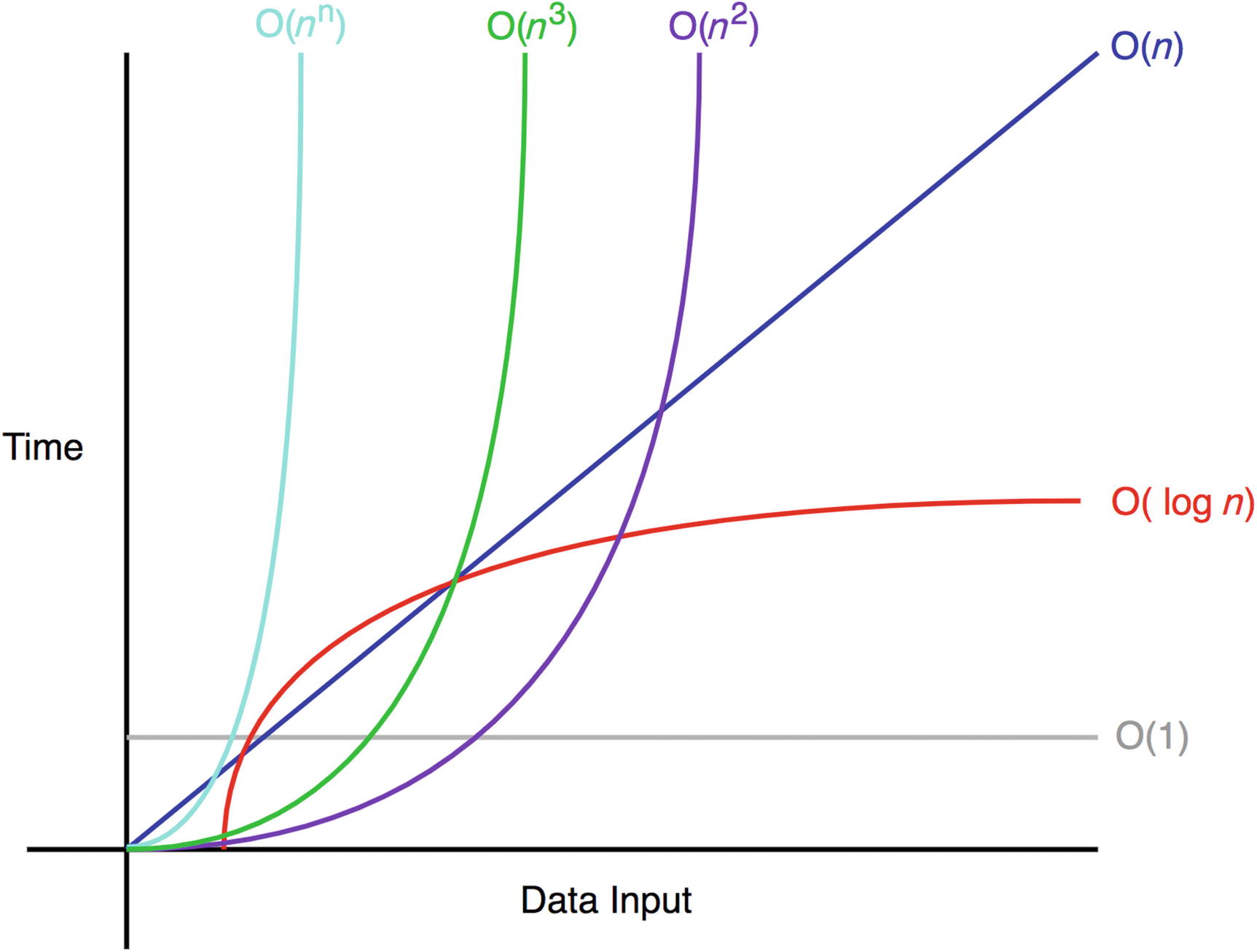
- O(1): 상수형 빅오, 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘
- O(logn): 로그형 빅오, 데이터 수의 증가율에 비해서 연산횟수의 증가율이 훨씬 낮은 알고리즘
- O(n): 선형 빅오, 데이터의 수와 연산횟수가 비례하는 알고리즘
- O(nlogn): 선형로그형 빅오, 데이터의 수가 두배로 늘 때, 연산횟수는 두 배를 조금 넘게 증가하는 알고리즘
- O(n²): 데이터 수의 제곱에 해당하는 연산횟수를 요구하는 알고리즘
- O(n³): 데이터 수의 세 제곱에 해당하는 연산횟수를 요구하는 알고리즘
728x90
'Data Structures & Algorithms' 카테고리의 다른 글
| [Data Structures] 트리 (Tree) (0) | 2022.05.07 |
|---|---|
| [Data Structures] 큐 (Queue)와 덱 (Deque) (0) | 2022.05.06 |
| [Data Structures] 스택 (Stack) (0) | 2022.05.06 |
| [Data Structures] 추상자료형 (Abstract Data Type) 과 리스트 자료구조 (0) | 2022.05.06 |
| [Data Structures] 재귀 (Recursion)의 이해 (0) | 2022.05.04 |